Skip to content

498. Diagonal Traverse

Description

Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.

 

Example 1:

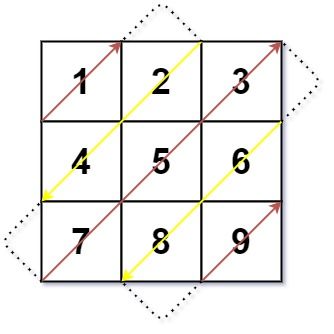
Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]

Example 2:

Input: mat = [[1,2],[3,4]]
Output: [1,2,3,4]

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 104
  • 1 <= m * n <= 104
  • -105 <= mat[i][j] <= 105

Solutions

Solution 1: Fixed Point Traversal

For each round \(k\), we fix the starting point from the top-right and traverse diagonally to the bottom-left to get \(t\). If \(k\) is even, we reverse \(t\).

The time complexity is \(O(m \times n)\), and the space complexity is \(O(1)\). Ignoring the space used for the answer.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        m, n = len(mat), len(mat[0])
        ans = []
        for k in range(m + n - 1):
            t = []
            i = 0 if k < n else k - n + 1
            j = k if k < n else n - 1
            while i < m and j >= 0:
                t.append(mat[i][j])
                i += 1
                j -= 1
            if k % 2 == 0:
                t = t[::-1]
            ans.extend(t)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[] ans = new int[m * n];
        int idx = 0;
        List<Integer> t = new ArrayList<>();
        for (int k = 0; k < m + n - 1; ++k) {
            int i = k < n ? 0 : k - n + 1;
            int j = k < n ? k : n - 1;
            while (i < m && j >= 0) {
                t.add(mat[i][j]);
                ++i;
                --j;
            }
            if (k % 2 == 0) {
                Collections.reverse(t);
            }
            for (int v : t) {
                ans[idx++] = v;
            }
            t.clear();
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
        int m = mat.size();
        int n = mat[0].size();
        vector<int> ans;
        vector<int> t;
        for (int k = 0; k < m + n - 1; ++k) {
            int i = (k < n) ? 0 : k - n + 1;
            int j = (k < n) ? k : n - 1;
            while (i < m && j >= 0) {
                t.push_back(mat[i][j]);
                ++i;
                --j;
            }
            if (k % 2 == 0) {
                ranges::reverse(t);
            }
            ans.insert(ans.end(), t.begin(), t.end());
            t.clear();
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func findDiagonalOrder(mat [][]int) []int {
    m := len(mat)
    n := len(mat[0])
    ans := make([]int, 0, m*n)
    for k := 0; k < m+n-1; k++ {
        t := make([]int, 0)
        var i, j int
        if k < n {
            i = 0
            j = k
        } else {
            i = k - n + 1
            j = n - 1
        }
        for i < m && j >= 0 {
            t = append(t, mat[i][j])
            i++
            j--
        }
        if k%2 == 0 {
            slices.Reverse(t)
        }
        ans = append(ans, t...)
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
function findDiagonalOrder(mat: number[][]): number[] {
    const m = mat.length;
    const n = mat[0].length;
    const ans: number[] = [];
    for (let k = 0; k < m + n - 1; k++) {
        const t: number[] = [];
        let i = k < n ? 0 : k - n + 1;
        let j = k < n ? k : n - 1;
        while (i < m && j >= 0) {
            t.push(mat[i][j]);
            i++;
            j--;
        }
        if (k % 2 === 0) {
            t.reverse();
        }
        ans.push(...t);
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
impl Solution {
    pub fn find_diagonal_order(mat: Vec<Vec<i32>>) -> Vec<i32> {
        let m = mat.len();
        let n = mat[0].len();
        let mut ans = Vec::with_capacity(m * n);
        for k in 0..(m + n - 1) {
            let mut t = Vec::new();
            let (mut i, mut j) = if k < n {
                (0, k)
            } else {
                (k - n + 1, n - 1)
            };
            while i < m && j < n {
                t.push(mat[i][j]);
                i += 1;
                if j == 0 { break; }
                j -= 1;
            }
            if k % 2 == 0 {
                t.reverse();
            }
            ans.extend(t);
        }
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class Solution {
    public int[] FindDiagonalOrder(int[][] mat) {
        int m = mat.Length;
        int n = mat[0].Length;
        List<int> ans = new List<int>();
        for (int k = 0; k < m + n - 1; k++) {
            List<int> t = new List<int>();
            int i = k < n ? 0 : k - n + 1;
            int j = k < n ? k : n - 1;
            while (i < m && j >= 0) {
                t.Add(mat[i][j]);
                i++;
                j--;
            }
            if (k % 2 == 0) {
                t.Reverse();
            }
            ans.AddRange(t);
        }
        return ans.ToArray();
    }
}

Comments