Skip to content

3656. Determine if a Simple Graph Exists πŸ”’

Description

You are given an integer array degrees, where degrees[i] represents the desired degree of the ith vertex.

Your task is to determine if there exists an undirected simple graph with exactly these vertex degrees.

A simple graph has no self-loops or parallel edges between the same pair of vertices.

Return true if such a graph exists, otherwise return false.

 

Example 1:

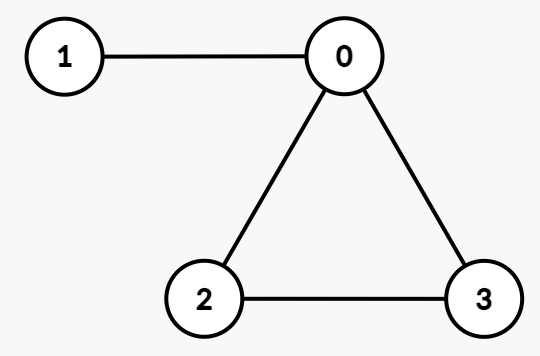
Input: degrees = [3,1,2,2]

Output: true

Explanation:

​​​​​​​

One possible undirected simple graph is:

  • Edges: (0, 1), (0, 2), (0, 3), (2, 3)
  • Degrees: deg(0) = 3, deg(1) = 1, deg(2) = 2, deg(3) = 2.

Example 2:

Input: degrees = [1,3,3,1]

Output: false

Explanation:​​​​​​​

  • degrees[1] = 3 and degrees[2] = 3 means they must be connected to all other vertices.
  • This requires degrees[0] and degrees[3] to be at least 2, but both are equal to 1, which contradicts the requirement.
  • Thus, the answer is false.

 

Constraints:

  • 1 <= n == degrees.length <= 10​​​​​​​5
  • 0 <= degrees[i] <= n - 1

Solutions

Solution 1

1


1


1


1

Comments