Skip to content

3623. Count Number of Trapezoids I

Description

You are given a 2D integer array points, where points[i] = [xi, yi] represents the coordinates of the ith point on the Cartesian plane.

A horizontal trapezoid is a convex quadrilateral with at least one pair of horizontal sides (i.e. parallel to the x-axis). Two lines are parallel if and only if they have the same slope.

Return the number of unique horizontal trapezoids that can be formed by choosing any four distinct points from points.

Since the answer may be very large, return it modulo 109 + 7.

 

Example 1:

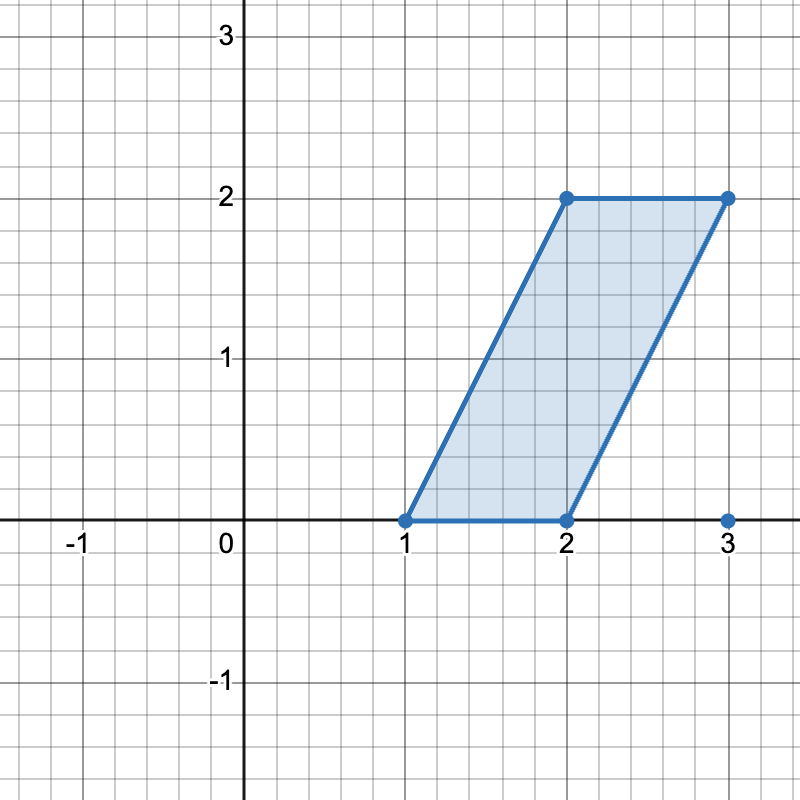
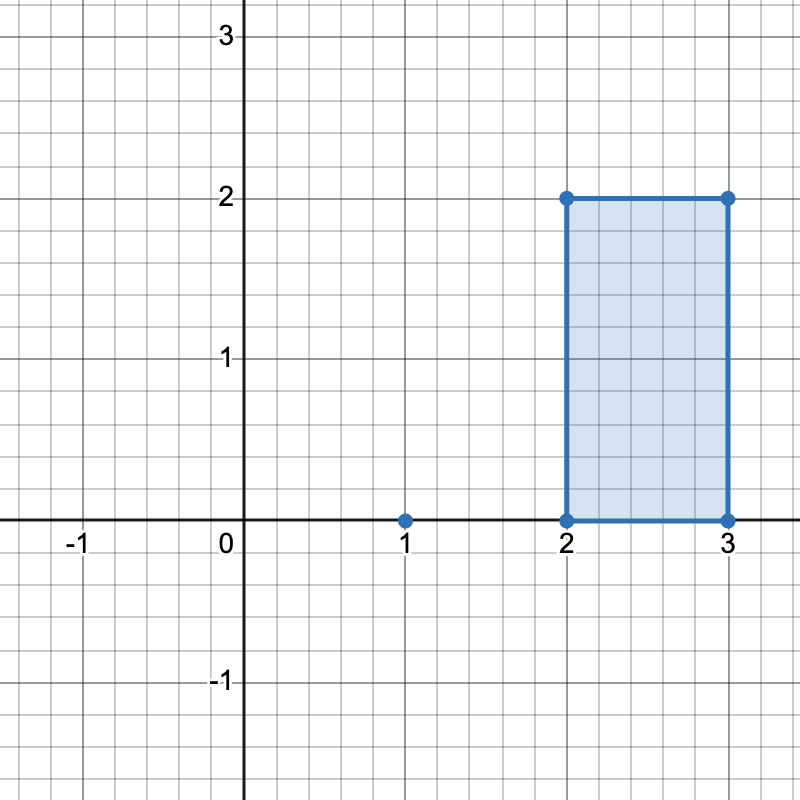
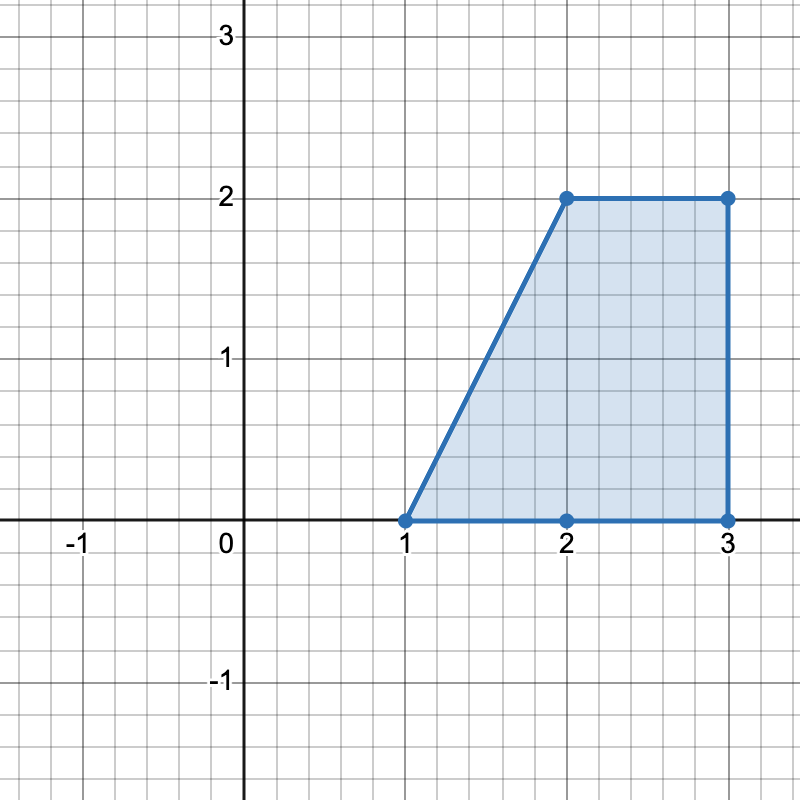
Input: points = [[1,0],[2,0],[3,0],[2,2],[3,2]]

Output: 3

Explanation:

There are three distinct ways to pick four points that form a horizontal trapezoid:

  • Using points [1,0], [2,0], [3,2], and [2,2].
  • Using points [2,0], [3,0], [3,2], and [2,2].
  • Using points [1,0], [3,0], [3,2], and [2,2].

Example 2:

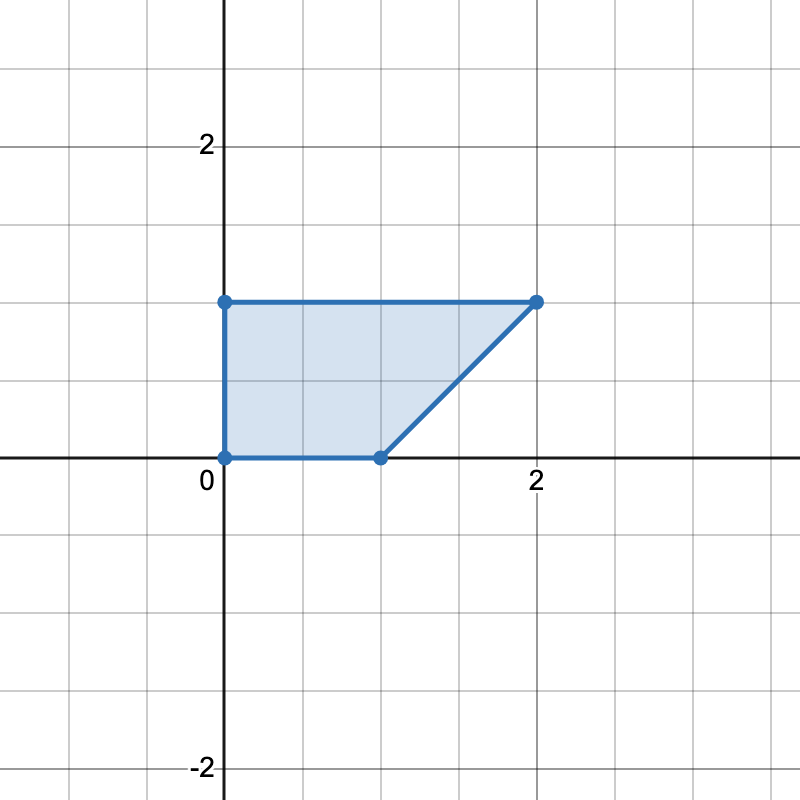
Input: points = [[0,0],[1,0],[0,1],[2,1]]

Output: 1

Explanation:

There is only one horizontal trapezoid that can be formed.

 

Constraints:

  • 4 <= points.length <= 105
  • –108 <= xi, yi <= 108
  • All points are pairwise distinct.

Solutions

Solution 1: Enumeration

According to the problem description, horizontal edges have the same \(y\) coordinate. Therefore, we can group points by their \(y\) coordinates and count the number of points for each \(y\) coordinate.

We use a hash table \(\textit{cnt}\) to store the number of points for each \(y\) coordinate. For each \(y\) coordinate \(y_i\), assuming the number of corresponding points is \(v\), the number of ways to select two points from these points as a horizontal edge is \(\binom{v}{2} = \frac{v(v-1)}{2}\), denoted as \(t\).

We use a variable \(s\) to record the sum of the number of horizontal edges for all previous \(y\) coordinates. Then, we can multiply the number of horizontal edges \(t\) for the current \(y\) coordinate by the sum \(s\) of the number of horizontal edges for all previous \(y\) coordinates to get the number of trapezoids with the current \(y\) coordinate as one pair of horizontal edges, and add it to the answer. Finally, we add the number of horizontal edges \(t\) for the current \(y\) coordinate to \(s\) for subsequent calculations.

Note that since the answer may be very large, we need to take the modulo \(10^9 + 7\).

The time complexity is \(O(n)\) and the space complexity is \(O(n)\), where \(n\) is the number of points.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
class Solution:
    def countTrapezoids(self, points: List[List[int]]) -> int:
        mod = 10**9 + 7
        cnt = Counter(p[1] for p in points)
        ans = s = 0
        for v in cnt.values():
            t = v * (v - 1) // 2
            ans = (ans + s * t) % mod
            s += t
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public int countTrapezoids(int[][] points) {
        final int mod = (int) 1e9 + 7;
        Map<Integer, Integer> cnt = new HashMap<>();
        for (var p : points) {
            cnt.merge(p[1], 1, Integer::sum);
        }
        long ans = 0, s = 0;
        for (int v : cnt.values()) {
            long t = 1L * v * (v - 1) / 2;
            ans = (ans + s * t) % mod;
            s += t;
        }
        return (int) ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    int countTrapezoids(vector<vector<int>>& points) {
        const int mod = 1e9 + 7;
        unordered_map<int, int> cnt;
        for (auto& p : points) {
            cnt[p[1]]++;
        }
        long long ans = 0, s = 0;
        for (auto& [_, v] : cnt) {
            long long t = 1LL * v * (v - 1) / 2;
            ans = (ans + s * t) % mod;
            s += t;
        }
        return (int) ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
func countTrapezoids(points [][]int) int {
    const mod = 1_000_000_007
    cnt := make(map[int]int)
    for _, p := range points {
        cnt[p[1]]++
    }

    var ans, s int64
    for _, v := range cnt {
        t := int64(v) * int64(v-1) / 2
        ans = (ans + s*t) % mod
        s += t
    }
    return int(ans)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function countTrapezoids(points: number[][]): number {
    const mod = 1_000_000_007;
    const cnt = new Map<number, number>();

    for (const p of points) {
        cnt.set(p[1], (cnt.get(p[1]) ?? 0) + 1);
    }

    let ans = 0;
    let s = 0;
    for (const v of cnt.values()) {
        const t = (v * (v - 1)) / 2;
        const mul = BigInt(s) * BigInt(t);
        ans = Number((BigInt(ans) + mul) % BigInt(mod));
        s += t;
    }

    return ans;
}

Comments