Skip to content

3244. Shortest Distance After Road Addition Queries II

Description

You are given an integer n and a 2D integer array queries.

There are n cities numbered from 0 to n - 1. Initially, there is a unidirectional road from city i to city i + 1 for all 0 <= i < n - 1.

queries[i] = [ui, vi] represents the addition of a new unidirectional road from city ui to city vi. After each query, you need to find the length of the shortest path from city 0 to city n - 1.

There are no two queries such that queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1].

Return an array answer where for each i in the range [0, queries.length - 1], answer[i] is the length of the shortest path from city 0 to city n - 1 after processing the first i + 1 queries.

 

Example 1:

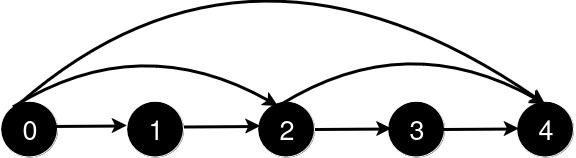
Input: n = 5, queries = [[2,4],[0,2],[0,4]]

Output: [3,2,1]

Explanation:

After the addition of the road from 2 to 4, the length of the shortest path from 0 to 4 is 3.

After the addition of the road from 0 to 2, the length of the shortest path from 0 to 4 is 2.

After the addition of the road from 0 to 4, the length of the shortest path from 0 to 4 is 1.

Example 2:

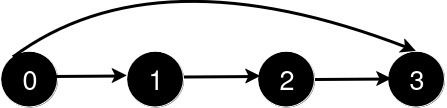
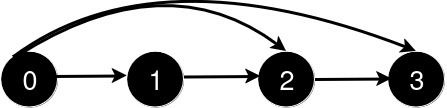
Input: n = 4, queries = [[0,3],[0,2]]

Output: [1,1]

Explanation:

After the addition of the road from 0 to 3, the length of the shortest path from 0 to 3 is 1.

After the addition of the road from 0 to 2, the length of the shortest path remains 1.

 

Constraints:

  • 3 <= n <= 105
  • 1 <= queries.length <= 105
  • queries[i].length == 2
  • 0 <= queries[i][0] < queries[i][1] < n
  • 1 < queries[i][1] - queries[i][0]
  • There are no repeated roads among the queries.
  • There are no two queries such that i != j and queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1].

Solutions

Solution 1: Greedy + Recording Jump Positions

We define an array \(\textit{nxt}\) of length \(n - 1\), where \(\textit{nxt}[i]\) represents the next city that can be reached from city \(i\). Initially, \(\textit{nxt}[i] = i + 1\).

For each query \([u, v]\), if \(u'\) and \(v'\) have already been connected before, and \(u' \leq u < v \leq v'\), then we can skip this query. Otherwise, we need to set the next city number for cities from \(\textit{nxt}[u]\) to \(\textit{nxt}[v - 1]\) to \(0\), and set \(\textit{nxt}[u]\) to \(v\).

During this process, we maintain a variable \(\textit{cnt}\), which represents the length of the shortest path from city \(0\) to city \(n - 1\). Initially, \(\textit{cnt} = n - 1\). Each time we set the next city number for cities in \([\textit{nxt}[u], \textit{v})\) to \(0\), \(\textit{cnt}\) decreases by \(1\).

Time complexity is \(O(n + q)\), and space complexity is \(O(n)\). Here, \(n\) and \(q\) are the number of cities and the number of queries, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def shortestDistanceAfterQueries(
        self, n: int, queries: List[List[int]]
    ) -> List[int]:
        nxt = list(range(1, n))
        ans = []
        cnt = n - 1
        for u, v in queries:
            if 0 < nxt[u] < v:
                i = nxt[u]
                while i < v:
                    cnt -= 1
                    nxt[i], i = 0, nxt[i]
                nxt[u] = v
            ans.append(cnt)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int[] shortestDistanceAfterQueries(int n, int[][] queries) {
        int[] nxt = new int[n - 1];
        for (int i = 1; i < n; ++i) {
            nxt[i - 1] = i;
        }
        int m = queries.length;
        int cnt = n - 1;
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            int u = queries[i][0], v = queries[i][1];
            if (nxt[u] > 0 && nxt[u] < v) {
                int j = nxt[u];
                while (j < v) {
                    --cnt;
                    int t = nxt[j];
                    nxt[j] = 0;
                    j = t;
                }
                nxt[u] = v;
            }
            ans[i] = cnt;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        vector<int> nxt(n - 1);
        iota(nxt.begin(), nxt.end(), 1);
        int cnt = n - 1;
        vector<int> ans;
        for (const auto& q : queries) {
            int u = q[0], v = q[1];
            if (nxt[u] && nxt[u] < v) {
                int i = nxt[u];
                while (i < v) {
                    --cnt;
                    int t = nxt[i];
                    nxt[i] = 0;
                    i = t;
                }
                nxt[u] = v;
            }
            ans.push_back(cnt);
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
func shortestDistanceAfterQueries(n int, queries [][]int) (ans []int) {
    nxt := make([]int, n-1)
    for i := range nxt {
        nxt[i] = i + 1
    }
    cnt := n - 1
    for _, q := range queries {
        u, v := q[0], q[1]
        if nxt[u] > 0 && nxt[u] < v {
            i := nxt[u]
            for i < v {
                cnt--
                nxt[i], i = 0, nxt[i]
            }
            nxt[u] = v
        }
        ans = append(ans, cnt)
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
function shortestDistanceAfterQueries(n: number, queries: number[][]): number[] {
    const nxt: number[] = Array.from({ length: n - 1 }, (_, i) => i + 1);
    const ans: number[] = [];
    let cnt = n - 1;
    for (const [u, v] of queries) {
        if (nxt[u] && nxt[u] < v) {
            let i = nxt[u];
            while (i < v) {
                --cnt;
                [nxt[i], i] = [0, nxt[i]];
            }
            nxt[u] = v;
        }
        ans.push(cnt);
    }
    return ans;
}

Comments