2106. Maximum Fruits Harvested After at Most K Steps

Description

Fruits are available at some positions on an infinite x-axis. You are given a 2D integer array fruits where fruits[i] = [position_i, amount_i] depicts amount_i fruits at the position position_i. fruits is already sorted by position_i in ascending order, and each position_i is unique.

You are also given an integer startPos and an integer k. Initially, you are at the position startPos. From any position, you can either walk to the left or right. It takes one step to move one unit on the x-axis, and you can walk at most k steps in total. For every position you reach, you harvest all the fruits at that position, and the fruits will disappear from that position.

Return the maximum total number of fruits you can harvest.

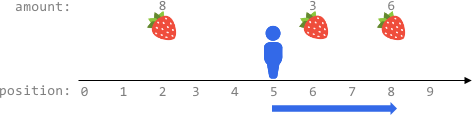
Example 1:

Input: fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
Output: 9
Explanation: 
The optimal way is to:
- Move right to position 6 and harvest 3 fruits
- Move right to position 8 and harvest 6 fruits
You moved 3 steps and harvested 3 + 6 = 9 fruits in total.

Example 2:

Input: fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
Output: 14
Explanation: 
You can move at most k = 4 steps, so you cannot reach position 0 nor 10.
The optimal way is to:
- Harvest the 7 fruits at the starting position 5
- Move left to position 4 and harvest 1 fruit
- Move right to position 6 and harvest 2 fruits
- Move right to position 7 and harvest 4 fruits
You moved 1 + 3 = 4 steps and harvested 7 + 1 + 2 + 4 = 14 fruits in total.

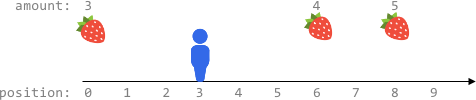
Example 3:

Input: fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
Output: 0
Explanation:
You can move at most k = 2 steps and cannot reach any position with fruits.

Constraints:

1 <= fruits.length <= 10⁵
fruits[i].length == 2
0 <= startPos, position_i <= 2 * 10⁵
position_i-1 < position_i for any i > 0 (0-indexed)
1 <= amount_i <= 10⁴
0 <= k <= 2 * 10⁵

Solutions

Solution 1: Two Pointers

Let's assume the movement range is \([l, r]\) and the starting position is \(\textit{startPos}\). We need to calculate the minimum number of steps required. Based on the position of \(\textit{startPos}\), we can divide this into three cases:

If \(\textit{startPos} \leq l\), then we move right from \(\textit{startPos}\) to \(r\). The minimum number of steps is \(r - \textit{startPos}\);
If \(\textit{startPos} \geq r\), then we move left from \(\textit{startPos}\) to \(l\). The minimum number of steps is \(\textit{startPos} - l\);
If \(l < \textit{startPos} < r\), we can either move left from \(\textit{startPos}\) to \(l\) then right to \(r\), or move right from \(\textit{startPos}\) to \(r\) then left to \(l\). The minimum number of steps is \(r - l + \min(\lvert \textit{startPos} - l \rvert, \lvert r - \textit{startPos} \rvert)\).

All three cases can be unified by the formula \(r - l + \min(\lvert \textit{startPos} - l \rvert, \lvert r - \textit{startPos} \rvert)\).

Suppose we fix the right endpoint \(r\) of the interval and move the left endpoint \(l\) to the right. Let's see how the minimum number of steps changes:

If \(\textit{startPos} \leq l\), as \(l\) increases, the minimum number of steps remains unchanged.
If \(\textit{startPos} > l\), as \(l\) increases, the minimum number of steps decreases.

Therefore, as \(l\) increases, the minimum number of steps is non-strictly monotonically decreasing. Based on this, we can use the two-pointer approach to find all qualifying maximum intervals, then take the one with the maximum total fruits among all qualifying intervals as the answer.

Specifically, we use two pointers \(i\) and \(j\) to point to the left and right indices of the interval, initially \(i = j = 0\). We also use a variable \(s\) to record the total number of fruits in the interval, initially \(s = 0\).

Each time we include \(j\) in the interval, then update \(s = s + \textit{fruits}[j][1]\). If the minimum number of steps in the current interval \(\textit{fruits}[j][0] - \textit{fruits}[i][0] + \min(\lvert \textit{startPos} - \textit{fruits}[i][0] \rvert, \lvert \textit{startPos} - \textit{fruits}[j][0] \rvert)\) is greater than \(k\), we move \(i\) to the right in a loop until \(i > j\) or the minimum number of steps in the interval is less than or equal to \(k\). At this point, we update the answer \(\textit{ans} = \max(\textit{ans}, s)\). Continue moving \(j\) until \(j\) reaches the end of the array.

Finally, return the answer.

The time complexity is \(O(n)\), where \(n\) is the length of the array. The space complexity is \(O(1)\).

Python3JavaC++GoTypeScriptRust

class Solution:
    def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:
        ans = i = s = 0
        for j, (pj, fj) in enumerate(fruits):
            s += fj
            while (
                i <= j
                and pj
                - fruits[i][0]
                + min(abs(startPos - fruits[i][0]), abs(startPos - fruits[j][0]))
                > k
            ):
                s -= fruits[i][1]
                i += 1
            ans = max(ans, s)
        return ans

class Solution {
    public int maxTotalFruits(int[][] fruits, int startPos, int k) {
        int ans = 0, s = 0;
        for (int i = 0, j = 0; j < fruits.length; ++j) {
            int pj = fruits[j][0], fj = fruits[j][1];
            s += fj;
            while (i <= j
                && pj - fruits[i][0]
                        + Math.min(Math.abs(startPos - fruits[i][0]), Math.abs(startPos - pj))
                    > k) {
                s -= fruits[i++][1];
            }
            ans = Math.max(ans, s);
        }
        return ans;
    }
}

class Solution {
public:
    int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
        int ans = 0, s = 0;
        for (int i = 0, j = 0; j < fruits.size(); ++j) {
            int pj = fruits[j][0], fj = fruits[j][1];
            s += fj;
            while (i <= j && pj - fruits[i][0] + min(abs(startPos - fruits[i][0]), abs(startPos - pj)) > k) {
                s -= fruits[i++][1];
            }
            ans = max(ans, s);
        }
        return ans;
    }
};

func maxTotalFruits(fruits [][]int, startPos int, k int) (ans int) {
    var s, i int
    for j, f := range fruits {
        s += f[1]
        for i <= j && f[0]-fruits[i][0]+min(abs(startPos-fruits[i][0]), abs(startPos-f[0])) > k {
            s -= fruits[i][1]
            i += 1
        }
        ans = max(ans, s)
    }
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

function maxTotalFruits(fruits: number[][], startPos: number, k: number): number {
    let ans = 0;
    let s = 0;
    for (let i = 0, j = 0; j < fruits.length; ++j) {
        const [pj, fj] = fruits[j];
        s += fj;
        while (
            i <= j &&
            pj -
                fruits[i][0] +
                Math.min(Math.abs(startPos - fruits[i][0]), Math.abs(startPos - pj)) >
                k
        ) {
            s -= fruits[i++][1];
        }
        ans = Math.max(ans, s);
    }
    return ans;
}

impl Solution {
    pub fn max_total_fruits(fruits: Vec<Vec<i32>>, start_pos: i32, k: i32) -> i32 {
        let mut ans = 0;
        let mut s = 0;
        let mut i = 0;
        for j in 0..fruits.len() {
            let pj = fruits[j][0];
            let fj = fruits[j][1];
            s += fj;
            while i <= j && pj - fruits[i][0] + std::cmp::min((start_pos - fruits[i][0]).abs(), (start_pos - pj).abs()) > k {
                s -= fruits[i][1];
                i += 1;
            }
            ans = ans.max(s)
        }
        ans
    }
}

2106. Maximum Fruits Harvested After at Most K Steps

Description

Solutions

Solution 1: Two Pointers

Comments