Skip to content

1578. Minimum Time to Make Rope Colorful

Description

Alice has n balloons arranged on a rope. You are given a 0-indexed string colors where colors[i] is the color of the ith balloon.

Alice wants the rope to be colorful. She does not want two consecutive balloons to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it colorful. You are given a 0-indexed integer array neededTime where neededTime[i] is the time (in seconds) that Bob needs to remove the ith balloon from the rope.

Return the minimum time Bob needs to make the rope colorful.

 

Example 1:

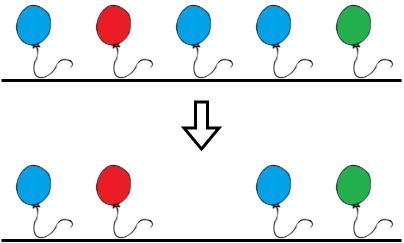
Input: colors = "abaac", neededTime = [1,2,3,4,5]
Output: 3
Explanation: In the above image, 'a' is blue, 'b' is red, and 'c' is green.
Bob can remove the blue balloon at index 2. This takes 3 seconds.
There are no longer two consecutive balloons of the same color. Total time = 3.

Example 2:

Input: colors = "abc", neededTime = [1,2,3]
Output: 0
Explanation: The rope is already colorful. Bob does not need to remove any balloons from the rope.

Example 3:

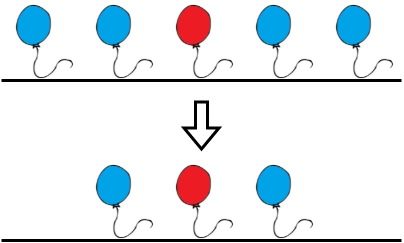
Input: colors = "aabaa", neededTime = [1,2,3,4,1]
Output: 2
Explanation: Bob will remove the balloons at indices 0 and 4. Each balloons takes 1 second to remove.
There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.

 

Constraints:

  • n == colors.length == neededTime.length
  • 1 <= n <= 105
  • 1 <= neededTime[i] <= 104
  • colors contains only lowercase English letters.

Solutions

Solution 1: Two Pointers + Greedy

We can use two pointers to point to the beginning and end of the current consecutive balloons with the same color, then calculate the total time \(s\) of these consecutive balloons with the same color, as well as the maximum time \(mx\). If the number of consecutive balloons with the same color is greater than \(1\), we can greedily choose to keep the balloon with the maximum time and remove the other balloons with the same color, which takes time \(s - mx\), and add it to the answer. Then we continue to traverse until all balloons are traversed.

The time complexity is \(O(n)\) and the space complexity is \(O(1)\), where \(n\) is the number of balloons.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def minCost(self, colors: str, neededTime: List[int]) -> int:
        ans = i = 0
        n = len(colors)
        while i < n:
            j = i
            s = mx = 0
            while j < n and colors[j] == colors[i]:
                s += neededTime[j]
                if mx < neededTime[j]:
                    mx = neededTime[j]
                j += 1
            if j - i > 1:
                ans += s - mx
            i = j
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int minCost(String colors, int[] neededTime) {
        int ans = 0;
        int n = neededTime.length;
        for (int i = 0, j = 0; i < n; i = j) {
            j = i;
            int s = 0, mx = 0;
            while (j < n && colors.charAt(j) == colors.charAt(i)) {
                s += neededTime[j];
                mx = Math.max(mx, neededTime[j]);
                ++j;
            }
            if (j - i > 1) {
                ans += s - mx;
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int minCost(string colors, vector<int>& neededTime) {
        int ans = 0;
        int n = colors.size();
        for (int i = 0, j = 0; i < n; i = j) {
            j = i;
            int s = 0, mx = 0;
            while (j < n && colors[j] == colors[i]) {
                s += neededTime[j];
                mx = max(mx, neededTime[j]);
                ++j;
            }
            if (j - i > 1) {
                ans += s - mx;
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
func minCost(colors string, neededTime []int) (ans int) {
    n := len(colors)
    for i, j := 0, 0; i < n; i = j {
        j = i
        s, mx := 0, 0
        for j < n && colors[j] == colors[i] {
            s += neededTime[j]
            mx = max(mx, neededTime[j])
            j++
        }
        if j-i > 1 {
            ans += s - mx
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function minCost(colors: string, neededTime: number[]): number {
    let ans = 0;
    const n = neededTime.length;

    for (let i = 0, j = 0; i < n; i = j) {
        j = i;
        let [s, mx] = [0, 0];
        while (j < n && colors[j] === colors[i]) {
            s += neededTime[j];
            mx = Math.max(mx, neededTime[j]);
            ++j;
        }
        if (j - i > 1) {
            ans += s - mx;
        }
    }

    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
impl Solution {
    pub fn min_cost(colors: String, needed_time: Vec<i32>) -> i32 {
        let n = needed_time.len();
        let mut ans = 0;
        let bytes = colors.as_bytes();
        let mut i = 0;

        while i < n {
            let mut j = i;
            let mut s = 0;
            let mut mx = 0;

            while j < n && bytes[j] == bytes[i] {
                s += needed_time[j];
                mx = mx.max(needed_time[j]);
                j += 1;
            }

            if j - i > 1 {
                ans += s - mx;
            }
            i = j;
        }

        ans
    }
}

Comments