119. Pascal's Triangle II

Description

Given an integer rowIndex, return the rowIndex^th (0-indexed) row of the Pascal's triangle.

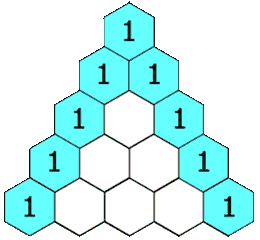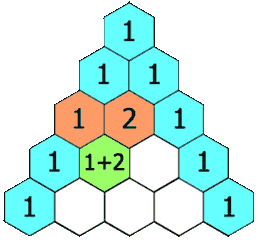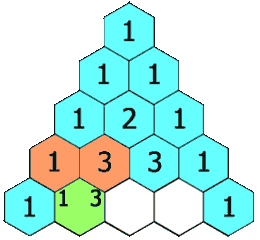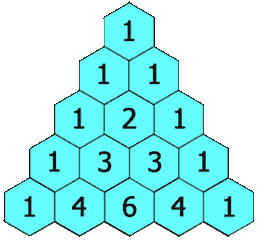
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:

Example 1:

Input: rowIndex = 3
Output: [1,3,3,1]

Example 2:

Input: rowIndex = 0
Output: [1]

Example 3:

Input: rowIndex = 1
Output: [1,1]

Constraints:

0 <= rowIndex <= 33

Follow up: Could you optimize your algorithm to use only O(rowIndex) extra space?

Solutions

Solution 1: Recursion

We create an array \(f\) of length \(rowIndex + 1\), initially all elements are \(1\).

Next, starting from the second row, we calculate the value of the \(j\)th element in the current row from back to front, \(f[j] = f[j] + f[j - 1]\), where \(j \in [1, i - 1]\).

Finally, return \(f\).

The time complexity is \(O(n^2)\), and the space complexity is \(O(n)\). Here, \(n\) is the given number of rows.

Python3JavaC++GoTypeScriptRustJavaScript

class Solution:
    def getRow(self, rowIndex: int) -> List[int]:
        f = [1] * (rowIndex + 1)
        for i in range(2, rowIndex + 1):
            for j in range(i - 1, 0, -1):
                f[j] += f[j - 1]
        return f

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> f = new ArrayList<>();
        for (int i = 0; i < rowIndex + 1; ++i) {
            f.add(1);
        }
        for (int i = 2; i < rowIndex + 1; ++i) {
            for (int j = i - 1; j > 0; --j) {
                f.set(j, f.get(j) + f.get(j - 1));
            }
        }
        return f;
    }
}

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> f(rowIndex + 1, 1);
        for (int i = 2; i < rowIndex + 1; ++i) {
            for (int j = i - 1; j; --j) {
                f[j] += f[j - 1];
            }
        }
        return f;
    }
};

func getRow(rowIndex int) []int {
    f := make([]int, rowIndex+1)
    for i := range f {
        f[i] = 1
    }
    for i := 2; i < rowIndex+1; i++ {
        for j := i - 1; j > 0; j-- {
            f[j] += f[j-1]
        }
    }
    return f
}

function getRow(rowIndex: number): number[] {
    const f: number[] = Array(rowIndex + 1).fill(1);
    for (let i = 2; i < rowIndex + 1; ++i) {
        for (let j = i - 1; j; --j) {
            f[j] += f[j - 1];
        }
    }
    return f;
}

impl Solution {
    pub fn get_row(row_index: i32) -> Vec<i32> {
        let n = (row_index + 1) as usize;
        let mut f = vec![1; n];
        for i in 2..n {
            for j in (1..i).rev() {
                f[j] += f[j - 1];
            }
        }
        f
    }
}

/**
 * @param {number} rowIndex
 * @return {number[]}
 */
var getRow = function (rowIndex) {
    const f = Array(rowIndex + 1).fill(1);
    for (let i = 2; i < rowIndex + 1; ++i) {
        for (let j = i - 1; j; --j) {
            f[j] += f[j - 1];
        }
    }
    return f;
};

119. Pascal's Triangle II

Description

Solutions

Solution 1: Recursion

Comments